Trong quy trình học tập toán, những câu hỏi với sự xuất hiện tại của hình tam giác vô cùng thông dụng. Việc chuẩn bị cho bản thân những kiến thức và kỹ năng về hình tam giác và công thức tính diện tích S tam giác là vô nằm trong quan trọng. Dưới trên đây, Truonghoc247 share về những loại tam giác thông thường gặp gỡ và công thức tính diện tích S của chúng!
Tam giác là gì?
Tam giác (hình tam giác) là một trong những nhập số những mô hình học tập cơ phiên bản và thông dụng. Hình tam giác với điểm lưu ý là hình phẳng lì nhập không khí 2 chiều, được kết cấu vì thế 3 điểm nối ko trực tiếp sản phẩm, 3 điểm là 3 đỉnh của tam giác, những đoạn trực tiếp nối 3 điểm đó là cạnh của tam giác. Tam giác là nhiều giác với không nhiều cạnh nhất (3 cạnh), tổng 3 góc nhập tam giác là 180 phỏng.
Bạn đang xem: diện tích tam giác tù
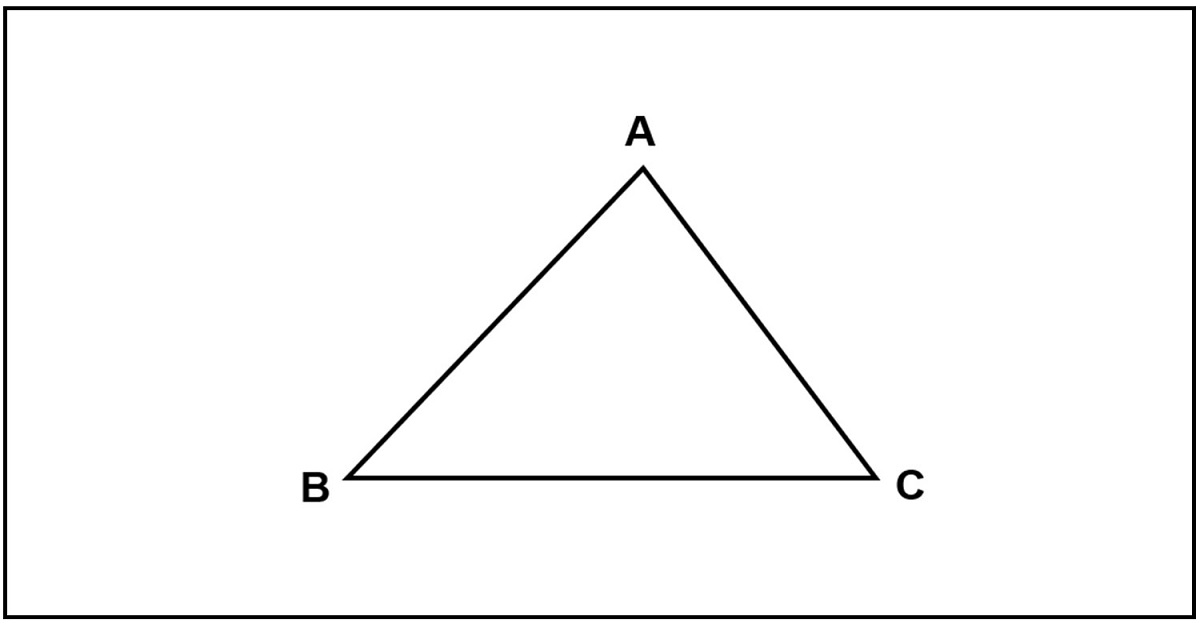
Ví dụ: Hình tam giác ABC bao gồm 3 cạnh (cạnh AB, BC, AC), 3 đỉnh (đỉnh A, B, C), 3 góc nhập (góc ABC, BCA, CAB). Dường như tam giác còn tồn tại 6 góc ngoài được tạo nên vì thế góc kề bù và góc nhập của tam giác.
Các loại tam giác thông thường gặp
Trong hình học tập, phụ thuộc những điểm riêng rẽ của cạnh tam giác, góc tam giác nhưng mà hình tam giác được chia nhỏ ra thực hiện nhiều loại như tam giác vuông, tam giác cân nặng, tam giác đều,… Trong toán học tập, việc xác lập những loại tam giác cũng vào vai trò vô cùng cần thiết nhằm tính đúng mực những độ dài rộng như diện tích S, chu vi hoặc phụ thuộc điểm lưu ý của từng loại tam giác nhằm suy đoán đặc điểm, cơ hội giải của câu hỏi. Dưới đó là những loại tam giác thông thường gặp:
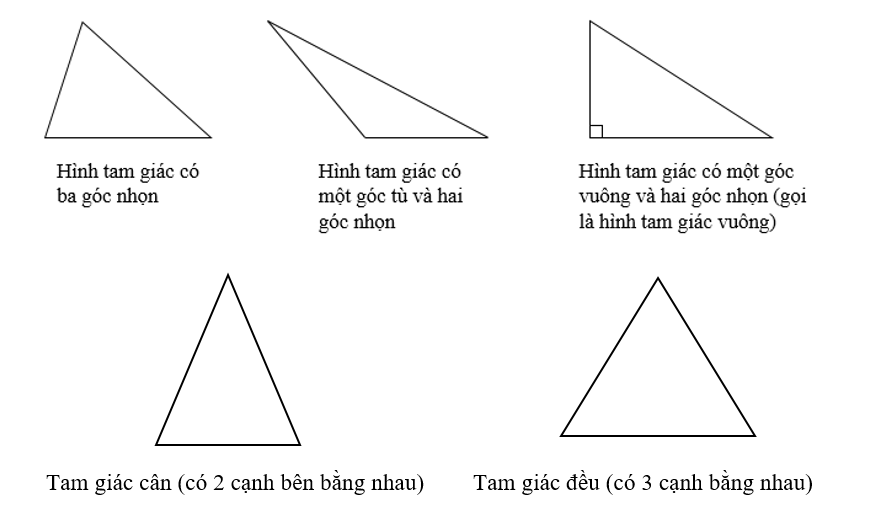
Tam giác thường
Tam giác thông thường là hình dạng tam giác cơ phiên bản nhất. Loại tam giác thông thường không tồn tại gì quan trọng, những cạnh với chiều nhiều năm không giống nhau, số đo những góc không giống nhau.
Tam giác tù
Tam giác tù là tam giác với cùng 1 góc là góc tù (góc to hơn 90 độ) và 2 góc còn sót lại là góc nhọn. Trong những dạng bài bác luyện thông thường không nhiều nói đến dạng tam giác này vì thế nó không tồn tại điểm lưu ý gì quá khác lạ đối với tam giác thông thường và nhiều khi còn được xem là một tam giác thông thường.
Tam giác nhọn
Tam giác nhọn là loại tam giác với 3 góc nhập đều là góc nhọn (góc nhỏ rộng lớn 90 độ). Tương tự động như tam giác tù, tam giác nhọn cũng không tồn tại điểm lưu ý, đặc điểm gì quan trọng và thông thường được đánh giá như tam giác thông thường trong số dạng bài bác luyện toán.
Tam giác vuông
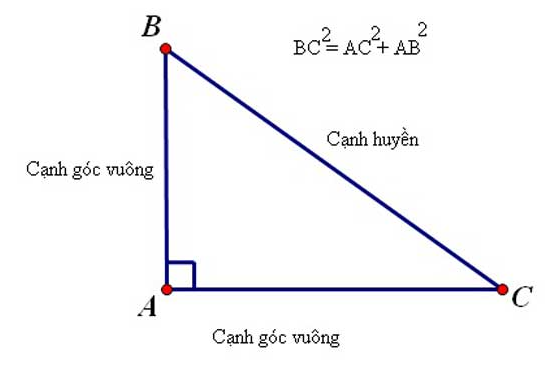
Tam giác vuông là hình tam giác có một góc là góc vuông (góc vì thế 90 độ). Trong tam giác vuông, cạnh đối lập góc vuông được gọi là cạnh huyền là cạnh với chiều nhiều năm lớn số 1 nhập tam giác, 2 cạnh tạo nên trở nên góc vuông gọi là cạnh góc vuông. Vì vẫn có một góc vuông vì thế 90 phỏng nên tổng 2 góc còn sót lại vì thế 90 phỏng.
Tam giác vuông xuất hiện tại thật nhiều trong số dạng bài bác luyện toán kể từ những lớp đái học tập tới trường 12. Định lý toán học tập nối sát với tam giác vuông là tấp tểnh lý pytago: “Bình phương cạnh huyền vì thế tổng bình phương nhì cạnh góc vuông”.
Ví dụ: Tam giác ABC vuông bên trên A với góc BAC = 90 phỏng. Theo tấp tểnh lý pytago: BC^2 = AB^2 + AC^2
Tam giác cân
Tam giác cân nặng là hình tam giác với chiều nhiều năm nhì cạnh không giống nhau gọi là nhì cạnh mặt mày, với 2 góc lòng cân nhau. 2 cạnh mặt mày dẫn đến 1 góc gọi đi ra góc ở đỉnh, 2 góc còn sót lại là 2 góc lòng. Với đặc điểm quan trọng cả về cạnh và góc nhập tam giác, tam giác cân nặng xuất hiện tại thông dụng nhập nhiều hình thức câu hỏi học tập.
Ngoài đi ra, tam giác cân nặng đàng cao kẻ kể từ đỉnh bên cạnh đó là đàng trung tuyến của tam giác cân nặng tiếp tục trải qua trung điểm của cạnh lòng.
Ví dụ: Tam giác ABC, cân nặng bên trên A với AB = AC, góc ABC = góc Ngân Hàng Á Châu, AH là đàng cao và là đàng trung tuyến của tam giác
Tam giác vuông cân
Như tên thường gọi, tam giác vuông cân nặng là tam giác quy tụ điểm lưu ý của tất cả tam giác vuông và tam giác cân nặng. Tam giác vuông cân nặng có một góc vuông (góc 90 độ), 2 cạnh góc vuông cân nhau, 2 góc lòng là 2 góc nhọn cân nhau và đều vì thế 45 phỏng. Trong tam giác vuông cân nặng, đàng cao, đàng trung tuyến, đàng phân giác kẻ kể từ đỉnh góc vuông trùng nhau và vì thế ½ cạnh huyền.
Ví dụ: Tam giác vuông cân nặng ABC, vuông cân nặng bên trên A với góc BAC vì thế 90 phỏng, góc ABC = góc Ngân Hàng Á Châu = 45 phỏng, cạnh AB = AC, cạnh BC là cạnh huyền và theo gót tấp tểnh lý pytago thì BC^2= AB^2 + AC^2. Đường cao AH là đàng phân giác, đàng trung tuyến của tam giác ABC và AH = ½ BC.
Tam giác đều
Tam giác đều là một trong những dạng tam giác quan trọng của tam giác cân nặng. Nếu tam giác cân nặng chỉ mất 2 cạnh mặt mày cân nhau và 2 góc lòng cân nhau thì tam giác đều sở hữu cả 3 cạnh tam giác cân nhau và 3 góc đều cân nhau (bằng 60 độ).
Ví dụ: Tam giác đều ABC với AB = BC = AC, góc ABC = góc BCA = góc BAC = 60 độ
Đường cao và lòng tam giác
Đường cao của tam giác là đoạn trực tiếp kẻ từ 1 đỉnh và vuông góc với cạnh đối lập của đỉnh cơ. Mỗi tam giác chỉ mất tía đàng cao. Ba đàng cao của một tam giác đồng quy bên trên một điểm thì điểm đó được gọi là trực tâm của hình tam giác.
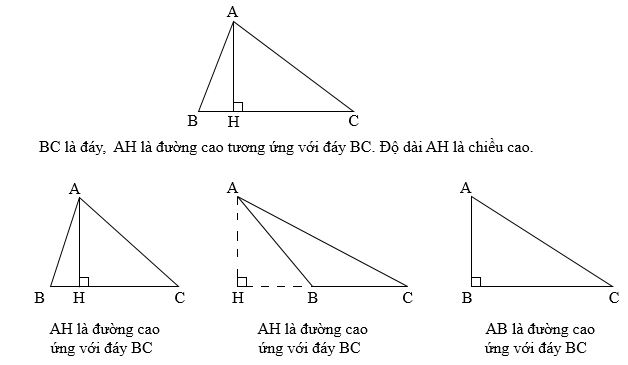
Một cạnh nhập tam giác được gọi là cạnh lòng khi cạnh cơ vuông góc với đàng cao nhập tam giác.
Diện tích tam giác thông thường được xem theo gót công thức: (chiều cao x cạnh đáy)/2
Ví dụ: Diện tích tam giác ABC với chiều nhiều năm lòng là 3m và độ cao là 2,1m. Diện tích tam giác ABC là: S= (3 * 2.1)/2 = 3.15 m2
Tuỳ theo gót từng cấp cho học tập và theo gót đề bài bác nhưng mà sẽ có được phương pháp tính diện tích S tam giác theo khá nhiều công thức không giống nhau như: tính diện tích S lúc biết 1 góc và chiều nhiều năm 2 cạnh kề hoặc tính diện tích S tam giác lúc biết phỏng nhiều năm 3 cạnh theo gót công thức Heron, tính diện tích S vì thế nửa đường kính đàng tròn trặn nước ngoài tiếp tam giác, tính diện tích S vì thế nửa đường kính đàng tròn trặn nội tiếp tam giác,…
Công thức tính diện tích S tam giác vuông
Công thức tính diện tích S tam giác vuông là: S= ½ ab, nhập cơ a, b đó là phỏng nhiều năm ứng của 2 cạnh góc vuông.
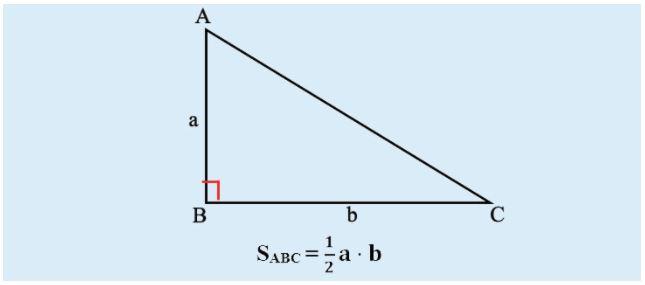
Ví dụ: Tam giác ABC vuông bên trên A với AB=3cm, AC= 4cm thì S= ½ * 3 * 4=6cm
Công thức tính diện tích S tam giác cân
Tam giác cân nặng với công thức tính tương tự động như tam giác thường: S = ½ *(a * h)
Trong đó: h là đàng cao kẻ từ một đỉnh của tam giác đều và a là chiều nhiều năm của cạnh đối mà đàng cao h trải qua.
Xem thêm: thiệp cưới ý tưởng (hồ văn huê quận phú nhuận)
Công thức tính diện tích S tam giác vuông cân
Tam giác vuông cân nặng với 2 cạnh góc vuông tiếp tục cân nhau và diện tích tam giác vuông cân sẽ tiến hành tính vì thế ½ a2, nhập cơ a đó là phỏng nhiều năm của cạnh góc vuông cân nặng.
Công thức tính diện tích S tam giác đều
Ngoài công thức tính diện tích S tam giác như tam giác thông thường, công thức tính diện tích S tam giác đều thông dụng trong không ít câu hỏi này đó là tấp tểnh lý Heron:
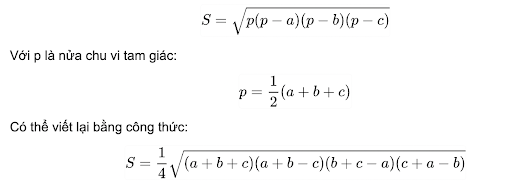
Công thức tính diện tích S tam giác nhập hệ toạ phỏng Oxyz
Khi học tập toán hình, ngoài các dạng toán đơn giản và giản dị nhập không khí 2 chiều thì sẽ có được những dạng toán nhập không khí 3 chiều. Khi cơ, tao cần thiết phần mềm công thức hệ trục toạ phỏng Oxyz nhằm tính diện tích S tam giác: SABC= ½ [AB;AC]
Trong cơ [AB;AC] được xem như sau:
Gọi tọa phỏng điểm A là A (a1, b1, c1); tọa phỏng điểm B là B (a2, b2, c2); tọa phỏng điểm C là C (a3, b3, c2). Theo cơ, AB = (a2-a1; b2-b1; c2-c1); AC = (a3-a1; b3-b1; c3-c1). Từ cơ tao với cơ hội tính: [AB;AC]= ( b2−b1 c2−c1) b3−b1 c3−c1 ; c2−c1 a2−a1 c3−c1 a3−a1; ; a2−a1 b2−b1 a3−a1 b3−b1 )
Sau cơ tất cả chúng ta trừ chéo cánh từng biểu thức lẫn nhau sẽ có được được thành quả của [AB;AC] là tọa phỏng bao gồm 3 điểm.
Một số dạng bài bác thói quen diện tích S tam giác
Dưới đó là một vài dạng bài bác thói quen diện tích S tam giác phổ biến:
Dạng 1: hiểu độ cao và phỏng nhiều năm lòng tính diện tích S tam giác
Ví dụ 1: Tính diện tích S tam giác thông thường ABC với chiều nhiều năm lòng BC=20cm và độ cao AH=13cm
Bài làm: Diện tích tam giác ABC = (20*13)/2= 130cm2
Ví dụ 2: Tính diện tích S tam giác vuông DEF vuông bên trên E với 2 cạnh góc vuông ED= 4dm, EF=5dm
Bài làm: Diện tích tam giác DEF = ½*4*5=10dm2
Dạng 2: Tính phỏng nhiều năm cạnh lòng lúc biết diện tích S và độ cao của tam giác
Từ công thức tính diện tích S tam giác S=(a*h)/2, suy ra sức thức tính phỏng nhiều năm cạnh lòng a=(S*2)/h
Ví dụ: Tính phỏng nhiều năm cạnh lòng BC của hình tam giác thông thường ABC với độ cao AH vì thế 10cm và diện tích S là 100cm2.
Bài làm: Độ nhiều năm BC=(100*2)/10=20cm
Dạng 3: Tính độ cao lúc biết diện tích S và phỏng nhiều năm đáy
Từ công thức tính diện tích S tam giác S=(a*h)/2, suy ra sức thức tính độ cao h=(S*2)/a
Ví dụ: Tính độ cao AH của hình tam giác ABC có tính nhiều năm cạnh lòng BC= 7cm và diện tích S vì thế 168cm2.
Bài làm: Chiều cao AH=(168*2)/7=12cm
Mẫu bài bác luyện tự động luyện diện tích S tam giác
Dưới đó là một vài bài bác luyện về tính chất diện tích S tam giác:
Bài 1:
Tính diện tích S tam giác có:
- Độ nhiều năm lòng là 13cm và độ cao là 8cm
- Độ nhiều năm lòng là 5.6dm và độ cao là 1 trong những.2dm
Đáp án:
- 52cm2
- 3.36cm2
Bài 2:
Tính diện tích S tam giác vuông có tính nhiều năm 2 cạnh góc vuông theo lần lượt là:
- 72cm và 24cm
- 11.4 centimet và 22.9cm
Đáp án:
Xem thêm: phim hành động mới 2016
- 864cm2
- 130.53cm2
Bài 3:
Cho hình tam giác BCD, biết phỏng nhiều năm lòng là 5m và độ cao là 4m. Tính diện tích S của tam giác BCD?
Đáp án: S=10m2
Trên đó là những công thức tính diện tích S tam giác thông dụng. Hy vọng những kiến thức và kỹ năng nhưng mà Truonghoc247 tổ hợp nhập nội dung bài viết này tiếp tục hữu ích với chúng ta.













Bình luận