Tam giác

Hình tam giác
Hình tam giác
Số cạnh và đỉnh	3
Ký hiệu Schläfli	{3} (đối với tam giác đều)
Diện tích	nhiều cơ hội (xem mặt mũi dưới)
Góc ngoài (độ)	60° (đối với tam giác đều)

Tam giác hoặc hình tam giác là 1 mô hình cơ bạn dạng vô hình học: hình hai phía phẳng phiu đem phụ vương đỉnh là phụ vương điểm ko trực tiếp sản phẩm và phụ vương cạnh là phụ vương đoạn trực tiếp nối những đỉnh cùng nhau. Tam giác là nhiều giác đem số cạnh tối thiểu (3 cạnh). Tam giác luôn luôn vẫn là một nhiều giác đơn và vẫn là một nhiều giác lồi (các góc vô luôn luôn nhỏ rộng lớn 180°). Một tam giác đem những cạnh AB, BC và AC được ký hiệu là ^[1].

Bạn đang xem: tam giác tù là gì

Từ nguyên[sửa | sửa mã nguồn]

Chữ Hán: 三角; nghĩa: "ba góc".

Các nguyên tố vô một tam giác[sửa | sửa mã nguồn]

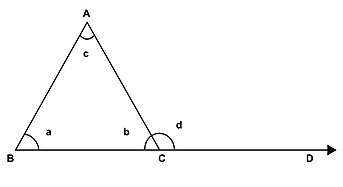
Góc vô Ngân Hàng Á Châu và góc ngoài ứng là ACD

Các góc vô một tam giác được gọi là góc vô. Các góc kề bù với góc vô được gọi là góc ngoài. Góc ngoài thì vày tổng những góc vô ko kề bù với nó. Mỗi tam giác chỉ mất 3 góc vô và 6 góc ngoài.

Các đàng đồng quy của tam giác[sửa | sửa mã nguồn]

Đường cao là 1 đoạn trực tiếp trải qua một đỉnh và vuông góc với cạnh đối lập của đỉnh cơ. Mỗi tam giác chỉ mất phụ vương đàng cao. Ba đàng cao của một tam giác đồng quy bên trên một điểm, đặc điểm đó được gọi là trực tâm của tam giác. Đường cao trải qua đỉnh góc vuông của một tam giác vuông thì tiếp tục phân tách tam giác ấy trở nên 2 tam giác đồng dạng với và nằm trong đồng dạng với tam giác vẫn cho tới.

Đường trung tuyến là 1 đoạn trực tiếp nối kể từ đỉnh cho tới trung điểm của cạnh đối lập. Một tam giác chỉ mất phụ vương đàng trung tuyến. Ba đàng trung tuyến của một tam giác đồng quy bên trên một điểm, đặc điểm đó được gọi là trọng tâm của tam giác. Khoảng cơ hội kể từ trọng tâm cho tới từng đỉnh vày đàng trung tuyến ứng với đỉnh cơ và suy rời khỏi, khoảng cách kể từ trọng tâm cho tới từng trung điểm vày đàng trung tuyến ứng với điểm cơ. Trên một phía phẳng phiu, đường thẳng liền mạch trải qua ngẫu nhiên một đỉnh và trọng tâm của tam giác đều thì phân tách tam giác cơ trở nên nhị tam giác đem diện tích S đều bằng nhau. Trong một tam giác, phụ vương trung tuyến phân tách tam giác cơ trở nên 6 tam giác đem diện tích S đều bằng nhau.

Tâm và đàng tròn trặn nước ngoài tiếp tam giác

Đường trung trực của một tam giác là đàng vuông góc với 1 cạnh của tam giác cơ bên trên trung điểm. Mỗi tam giác chỉ mất phụ vương đàng trung trực. Ba đàng trung trực của một tam giác đồng quy bên trên một điểm, điểm cơ mang tên gọi là tâm của đàng tròn trặn nước ngoài tiếp tam giác. Tâm của đàng tròn trặn nước ngoài tiếp tam giác cơ hội đều phụ vương đỉnh của tam giác cơ.

Đường phân giác là đoạn trực tiếp nối kể từ đỉnh cho tới cạnh đối lập và phân tách góc ở đỉnh thực hiện 2 phần đem số đo góc đều bằng nhau. Mỗi tam giác chỉ mất phụ vương đàng phân giác. Ba đàng này đồng quy bên trên một điểm. Điểm cơ mang tên gọi là tâm của đàng tròn trặn nội tiếp tam giác. Khoảng cơ hội kể từ tâm của đàng tròn trặn nội tiếp tam giác cho tới những cạnh là đều bằng nhau. Đường phân giác trải qua một góc của một đinh tam giác thì phân tách cạnh đối lập của góc cơ những đoạn tỉ lệ thành phần với nhị cạnh sót lại của tam giác.

Theo tấp tểnh lý Euler: Trong một tam giác: trực tâm, trọng tâm, tâm của đàng tròn trặn nước ngoài tiếp tam giác nằm trong lệ thuộc một đường thẳng liền mạch, trọng tâm tiếp tục nằm trong lòng trực tâm và tâm của đàng tròn trặn nước ngoài tiếp tam giác, kể từ trực tâm cho tới tâm của đàng tròn trặn nước ngoài tiếp tam giác tiếp tục vày 3 phen kể từ trọng tâm cho tới tâm của đàng tròn trặn nước ngoài tiếp tam giác. Đường trực tiếp chứa chấp phụ vương điểm này được gọi là đường thẳng liền mạch Euler.

Đối với những đàng đồng quy của một tam giác (đường cao, đàng trung tuyến, đàng trung trực, đàng phân giác), tao rất có thể đánh giá như sau:

Trọng tâm và tâm đàng tròn trặn nội tiếp luôn luôn trực tiếp ở trong tam giác.
Trực tâm ở ngoài tam giác Lúc này đó là tam giác tù, trùng với đỉnh góc vuông Lúc này đó là tam giác vuông, nằm cạnh trong những khi này đó là tam giác nhọn.
Tâm của đàng tròn trặn nước ngoài tiếp tam giác ở ngoài tam giác Lúc này đó là tam giác tù, trùng với cạnh (là trung điểm của cạnh huyền) Lúc này đó là tam giác vuông, nằm cạnh vô tam giác Lúc này đó là tam giác nhọn.
Trong một tam giác cân: trực tâm, trọng tâm, tâm của đàng tròn trặn nước ngoài tiếp tam giác, tâm của đàng tròn trặn nội tiếp tam giác tiếp tục trực tiếp sản phẩm cùng nhau. Đường trực tiếp cơ đó là đàng trung tuyến, đôi khi cũng chính là đàng phân giác, đàng trung trực và đàng cao ứng với cạnh lòng.
Trong một tam giác đều: trực tâm, trọng tâm, tâm của đàng tròn trặn nước ngoài tiếp tam giác, tâm của đàng tròn trặn nội tiếp tam giác trùng nhau. Các cặp đàng trung tuyến, đàng phân giác, đàng trung trực, đàng cao cũng trùng nhau.
Đường tầm của tam giác là đoạn trực tiếp nối nhị trung điểm của nhị cạnh vô một tam giác. Đường tầm đem tính chất: tuy vậy song với cạnh loại phụ vương và vày 50% cạnh loại phụ vương.

Sự đều bằng nhau Một trong những tam giác[sửa | sửa mã nguồn]

Hai tam giác được gọi là đều bằng nhau Lúc bọn chúng rất có thể bịa đặt trùng khít lên nhau sau một số trong những phép tắc tịnh tiến thủ, cù và đối xứng. Nói cách thứ hai nhị tam giác được gọi là đều bằng nhau nếu như bọn chúng đem những cạnh ứng đều bằng nhau và những góc ứng đều bằng nhau. Hai tam giác đều bằng nhau Lúc và chỉ Lúc vừa lòng 1 trong những bảy ĐK sau đây:

Hai tam giác đem phụ vương cặp cạnh ứng đều bằng nhau thì đều bằng nhau (cạnh-cạnh-cạnh).
Hai tam giác đem nhị cặp cạnh ngẫu nhiên ứng đều bằng nhau và cặp góc xen Một trong những cạnh cơ đều bằng nhau thì đều bằng nhau. (Cạnh-góc-cạnh).
Hai tam giác mang 1 cặp cạnh ngẫu nhiên đều bằng nhau và nhị cặp góc kề với cặp cạnh ấy đều bằng nhau thì đều bằng nhau .(Góc-cạnh-góc ).
Hai tam giác vuông đem cặp cạnh huyền và một cặp cạnh góc vuông đều bằng nhau thì đều bằng nhau. (Cạnh huyền-cạnh góc vuông).
Hai tam giác vuông đem cặp cạnh huyền và một cặp góc nhọn đều bằng nhau thì đều bằng nhau.(Cạnh huyền-góc nhọn).
Hai tam giác vuông đem nhị cặp cạnh góc vuông đều bằng nhau thì đều bằng nhau.(Cạnh góc vuông-cạnh góc vuông).
Hai tam giác vuông mang 1 cặp cạnh góc vuông và góc nhọn kề nó đều bằng nhau thì đều bằng nhau.(Cạnh góc vuông-góc nhọn).
Quan hệ đều bằng nhau Một trong những tam giác là tình huống đặc biệt quan trọng của mối quan hệ đồng dạng Một trong những tam giác Lúc những cạnh tỷ trọng nhau theo gót thông số tỷ trọng là một trong những.

Sự đồng dạng Một trong những tam giác[sửa | sửa mã nguồn]

Hai tam giác được gọi là đồng dạng nếu như 1 trong những bọn chúng vày với 1 tam giác cảm nhận được kể từ tam giác cơ sau đó 1 phép tắc vị tự động. Các ĐK cần thiết và đầy đủ nhằm nhị tam giác đồng dạng:

Hai tam giác có phụ vương cặp cạnh ứng tỷ trọng với nhau thì đồng dạng.(Cạnh-cạnh-cạnh).
Hai tam giác đem nhị cặp góc ứng đều bằng nhau thì đồng dạng. (Góc-góc).
Hai tam giác đem nhị cặp cạnh ứng tỷ trọng và góc xen thân thích nhị cặp cạnh ấy đều bằng nhau thì đồng dạng. (Cạnh-góc-cạnh).
Hai tam giác vuông đem cặp cạnh huyền và một cặp cạnh góc vuông ứng tỷ trọng thì đồng dạng.(Cạnh huyền-cạnh góc vuông).
Hai tam giác đều bằng nhau thì đồng dạng.

Các đặc thù của tam giác đồng dạng:

Tỉ số đồng dạng của nhị tam giác là tỷ số thân thích nhị cạnh ứng bất của nhị tam giác cơ Lúc bọn chúng đồng dạng

Tỉ số hai tuyến phố phân giác, hai tuyến phố cao, hai tuyến phố trung tuyến, hai tuyến phố tròn trặn nước ngoài tiếp tam giác, hai tuyến phố tròn trặn nội tiếp tam giác, nhị chu vi ứng của nhị tam giác đồng dạng vày tỉ số đồng dạng.
Tỉ số diện tích S của nhị tam giác đồng dạng vày bình phương tỉ số đồng dạng.

Phân loại tam giác[sửa | sửa mã nguồn]

Trong hình học tập Euclid, thuật ngữ "tam giác" thông thường được hiểu là tam giác phía trên một phía phẳng phiu. Trong khi còn tồn tại tam giác cầu vô hình học tập cầu, tam giác hyperbol vô hình học tập hyperbol. Tam giác phẳng phiu đem một số trong những dạng đặc biệt quan trọng, được xét theo gót đặc thù những cạnh và những góc của nó:

Theo phỏng nhiều năm những cạnh[sửa | sửa mã nguồn]

Tam giác thường là tam giác cơ bạn dạng nhất, có tính nhiều năm những cạnh không giống nhau, số đo góc vô cũng không giống nhau. Tam giác thông thường cũng rất có thể bao hàm những tình huống đặc biệt quan trọng của tam giác.
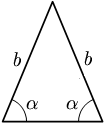
Tam giác cân là tam giác đem nhị cạnh đều bằng nhau, nhị cạnh này được gọi là nhị cạnh mặt mũi. Đỉnh của một tam giác cân nặng là gửi gắm điểm của nhị cạnh mặt mũi. Góc được tạo nên vày đỉnh được gọi là góc ở đỉnh, nhị góc sót lại gọi là góc ở lòng. Tính hóa học của tam giác cân nặng là nhị góc ở lòng thì đều bằng nhau.
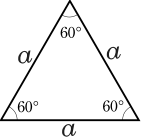
Tam giác đều là tình huống đặc biệt quan trọng của tam giác cân nặng đem cả phụ vương cạnh đều bằng nhau. Tính hóa học của tam giác đều là đem 3 góc đều bằng nhau và vày 60°.



Tam giác thường	Tam giác đều	Tam giác cân

Theo số đo những góc trong[sửa | sửa mã nguồn]

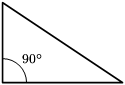
Tam giác vuông là tam giác mang 1 góc vày 90° (là góc vuông). Trong một tam giác vuông, cạnh đối lập với góc vuông gọi là cạnh huyền, là cạnh lớn số 1 vô tam giác cơ. Hai cạnh sót lại được gọi là cạnh góc vuông của tam giác vuông. Định lý Pythagoras là tấp tểnh lý phổ biến so với hình tam giác vuông, có tên mái ấm toán học tập lỗi lạc Pythagoras.
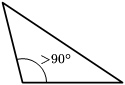
Tam giác tù là tam giác mang 1 góc vô to hơn rộng lớn rộng lớn 90° (một góc tù) hoặc mang 1 góc ngoài bé nhiều hơn 90° (một góc nhọn).
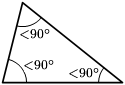
Tam giác nhọn là tam giác đem phụ vương góc vô đều nhỏ rộng lớn 90° (ba góc nhọn) hoặc đem toàn bộ góc ngoài to hơn 90° (sáu góc tù)



Tam giác vuông	Tam giác tù	Tam giác nhọn
Tam giác vuông	Tam giác thường

Tam giác vuông cân vừa vặn là tam giác vuông, vừa vặn là tam giác cân nặng. Trong một tam giác vuông cân nặng, nhị cạnh góc vuông đều bằng nhau và từng góc nhọn vày 45^°.

Một số đặc thù của tam giác (trong hình học tập Euclid)[sửa | sửa mã nguồn]

Tổng những góc vô của một tam giác vày 180° (định lý tổng phụ vương góc vô của một tam giác).
Độ nhiều năm từng cạnh to hơn hiệu phỏng nhiều năm nhị cạnh cơ và nhỏ rộng lớn tổng phỏng nhiều năm của bọn chúng (bất đẳng thức tam giác).
Trong một tam giác, cạnh đối lập với góc to hơn là cạnh to hơn. trái lại, góc đối lập với cạnh to hơn là góc to hơn (quan hệ thân thích cạnh và góc đối lập vô tam giác).
Ba đàng cao của tam giác hạn chế nhau bên trên một điểm được gọi là trực tâm của tam giác (đồng quy tam giác).
Ba đàng trung tuyến của tam giác hạn chế nhau bên trên một điểm. Điểm này được gọi là trọng tâm của tam giác. Hay hay còn gọi là phụ vương đàng trung tuyến của tam giác đồng quy bên trên một điểm( đồng quy bên trên một điểm Có nghĩa là nằm trong lên đường qua một điểm). Khoảng cơ hội kể từ trọng tâm cho tới 3 đỉnh của tam giác vày 2/3 phỏng nhiều năm đàng trung tuyến ứng với đỉnh cơ. Đường trung tuyến của tam giác phân tách tam giác trở nên nhị phần đem diện tích S đều bằng nhau (đồng quy tam giác).
Ba đàng trung trực của tam giác hạn chế nhau bên trên một điểm là tâm đàng tròn trặn nước ngoài tiếp của tam giác (đồng quy tam giác).
Ba đàng phân giác vô của tam giác hạn chế nhau bên trên một điểm là tâm đàng tròn trặn nội tiếp của tam giác (đồng quy tam giác).
Định lý hàm số cosin: Trong một tam giác, bình phương phỏng nhiều năm một cạnh vày tổng bình phương phỏng nhiều năm nhị canh sót lại trừ lên đường nhị phen tích của phỏng nhiều năm nhị cạnh ấy với cosin của góc xen thân thích nhị cạnh cơ.
Định lý hàm số sin: Trong một tam giác tỷ trọng thân thích phỏng nhiều năm của từng cạnh với sin của góc đối lập là như nhau cho tất cả phụ vương cạnh.
Đường tầm là đoạn trực tiếp nối trung điểm nhị cạnh của tam giác; một tam giác đem phụ vương đàng tầm. Đường tầm của tam giác thì tuy vậy song với cạnh loại phụ vương và có tính nhiều năm vày 50% phỏng nhiều năm cạnh cơ. Tam giác mới mẻ tạo nên vày phụ vương đàng tầm vô một tam giác thì nó đồng dạng với tam giác công ty của chính nó.
Trong tam giác, đàng phân giác của một góc phân tách cạnh đối lập trở nên 2 đoạn trực tiếp tỷ trọng với 2 cạnh kề 2 đoạn trực tiếp cơ.

Trong hình học tập phi Euclid thì một tam giác rất có thể đem tổng phụ vương góc tùy thuộc vào độ dài rộng của tam giác, Lúc độ dài rộng tam giác ngày càng tăng thì tổng cơ tiến thủ cho tới độ quý hiếm là 0 và đem diện tích S là vô hạn.

Trong hình học tập hyperbol, tổng phụ vương góc vô một tam giác nhỏ rộng lớn 180°.
Trong hình học tập mặt mũi cầu, tổng những góc vô của một tam giác cầu to hơn 180°.

Các công thức tính diện tích S tam giác[sửa | sửa mã nguồn]

Tính diện tích S tam giác là 1 câu hỏi cơ bạn dạng thông thường được bắt gặp vô hình học tập sơ cấp cho.

Bằng cơ hội dùng hình học[sửa | sửa mã nguồn]

Diện tích S vày ½bh, vô cơ b là phỏng nhiều năm của một cạnh ngẫu nhiên của tam giác (thường gọi là đáy) và h là phỏng nhiều năm đàng cao hạ kể từ đỉnh đối lập xuống cạnh ấy.

Có thể lý giải công thức này bằng phương pháp người sử dụng diện tích S hình chữ nhật như sau:

Xem thêm: quán cà phê đẹp ở vũng tàu

Diện tích tam giác vày 50% diện tích S hình bình hành, diện tích S hình bình hành vày diện tích S một hình chữ nhật.

Từ một tam giác (màu xanh rì lục), tao tiếp tục sao một tam giác vày nó,(màu xanh rì lam), cù góc 180°, và ghép bọn chúng trở nên hình bình hành. Cắt 1 phần của hình bình hành, ghép lại trở nên hình chữ nhật. Vì diện tích S hình chữ nhật là bh, nên diện tích S tam giác là ½bh.

Nói cách thứ hai, diện tích S tam giác vày phỏng nhiều năm cạnh lòng nhân với độ cao phân tách 2:

Đặc biệt

Tam giác vuông thì diện tích S tiếp tục tính là 1 nửa tích nhị cạnh góc vuông hoặc nửa tích đàng cao với cạnh huyền.

Tam giác đều thì diện tích S tiếp tục tính là bình phương 1 cạnh nhân với

Bằng cách sử dụng vectơ[sửa | sửa mã nguồn]

Diện tích hình bình hành là tích đem vị trí hướng của nhị vectơ.

Nếu tứ giác ABDC là hình bình hành thì diện tích S của chính nó được xem vày công thức:

trong cơ là tích đem vị trí hướng của nhị vectơ và .

Diện tích tam giác ABC vày 50% diện tích S của hình bình hành ABDC nên:

Bằng cách sử dụng lượng giác[sửa | sửa mã nguồn]

Diện tích tam giác vày nửa tích phỏng nhiều năm 2 cạnh nhân với sin của góc hợp ý vày 2 cạnh cơ.

Bằng cách thức người sử dụng tọa độ[sửa | sửa mã nguồn]

Nếu đỉnh A đặt tại gốc tọa phỏng (0, 0) của hệ tọa phỏng Descartes và tọa phỏng của nhị đỉnh cơ là B = (x_B, y_B) và C = (x_C, y_C), thì diện tích S S của tam giác ABC vày 50% của độ quý hiếm vô cùng của tấp tểnh thức

Trong tình huống tổng quát mắng, tao có:

Trong không khí phụ vương chiều, diện tích S của tam giác cho tới vày {A = (x_A, y_A, z_A), B = (x_B, y_B, z_B) và C = (x_C, y_C, z_C)} là tổng 'Pythagor' của những diện tích S những hình chiếu của bọn chúng bên trên những mặt mũi phẳng phiu tọa phỏng (nghĩa là x=0, y=0 and z=0):

Áp dụng công thức Heron[sửa | sửa mã nguồn]

Cũng rất có thể tính diện tích S tam giác S theo gót Công thức Heron:

trong cơ là nửa chu vi của tam giác.

Thông qua chuyện đàng tròn trặn nội tiếp[sửa | sửa mã nguồn]

Gọi r là nửa đường kính đàng tròn trặn nội tiếp tam giác và là nửa chu vi của tam giác, Lúc cơ

Thông qua chuyện đàng tròn trặn nước ngoài tiếp[sửa | sửa mã nguồn]

Gọi R là nửa đường kính đàng tròn trặn nước ngoài tiếp tam giác, Lúc cơ

Những phương pháp cơ bản[sửa | sửa mã nguồn]

Euclid vẫn trình diễn những phương pháp cơ bạn dạng về tam giác vô tập dượt 1 cho tới tập dượt 4 kiệt tác Cơ sở (Elements) của ông, viết lách khoảng tầm năm 300 TCN.

Tam giác là 1 nhiều giác và đơn hình bậc 2 (xem nhiều diện).

Hai tam giác là đồng dạng nếu như rất có thể khai triển (co hoặc giãn) tam giác này theo gót và một tỷ trọng để sở hữu tam giác cơ. Trường hợp ý này, phỏng nhiều năm của những mặt mũi đồng vị đem tỷ trọng đều bằng nhau. Tức là nhị tam giác đồng dạng cùng nhau, nếu như cạnh lớn số 1 của tam giác này hấp tấp từng nào phen cạnh lớn số 1 của tam giác cơ, thì cạnh nhỏ nhắn nhất của tam giác này cũng hấp tấp từng ấy phen cạnh nhỏ nhắn nhất của tam giác cơ và tương tự động với cạnh sót lại.

Hơn nữa, tỷ trọng cạnh nhiều năm bên trên cạnh cụt của một tam giác sẽ rất cần vày tỷ trọng cạnh nhiều năm bên trên cạnh cụt của tam giác cơ. Điều cần thiết là những góc đồng vị cần đều bằng nhau nhằm nhị tam giác được đồng dạng nhau. Việc này cũng xẩy ra nếu như một tam giác mang 1 cạnh công cộng với tam giác cơ, và những cạnh so với nó thì đều bằng nhau.

Hàm lượng giác sin và cosin rất có thể nắm vững khi sử dụng tam giác vuông và định nghĩa đồng dạng. Đó là nhị hàm của góc được nghiên cứu và phân tích bởi số lượng giác học tập.

Những tấp tểnh lý phổ biến được vận dụng vô tam giác[sửa | sửa mã nguồn]

Một số tấp tểnh lý phổ biến đem tương quan cho tới tam giác là:

Xem thêm: thả thính dễ thương

Định lý Pythagoras: Trong một tam giác vuông, bình phương cạnh huyền vày tổng bình phương của nhị cạnh góc vuông. Được viết lách vày hệ thức: c² = a² + b²
Định lý Apollonius: Với một tam giác ABC, và AD là đàng trung tuyến tao đem hệ thức: AB² + AC² = 2(AD² +BD²)
Định lý Stewart: Gọi a, b, và c là phỏng nhiều năm những cạnh của một tam giác. Gọi d là phỏng nhiều năm của đoạn trực tiếp nối từ là 1 đỉnh của tam giác với điểm phía trên cạnh (ở đấy là cạnh có tính nhiều năm là a) đối lập với đỉnh cơ. Đoạn trực tiếp này phân tách cạnh a trở nên nhị đoạn có tính nhiều năm m và n, tấp tểnh lý Stewart sẽ sở hữu được hệ thức: b²m + c²n = a(d² +mn)
Định lý Thales: Có một đường thẳng liền mạch hạn chế nhị cạnh của một tam giác và tuy vậy song với cạnh sót lại thì tiếp tục xuất hiện tại những cặp đoạn trực tiếp tỉ lệ thành phần bên trên nhị cạnh được hạn chế cơ.

Các dự án công trình phong cách thiết kế dùng hình tam giác[sửa | sửa mã nguồn]

Hiện ni, hình chữ nhật là 1 hình trạng học tập thịnh hành và thịnh hành nhất cho những dự án công trình vì như thế hình dạng dễ dàng xếp ông xã và bố trí, thiệt đơn giản và dễ dàng nhằm design loại thiết kế bên trong và đồ vật nhằm phù phù hợp với mặt mũi trong những tòa mái ấm hình chữ nhật. Hình tam giác, trong những khi khó khăn dùng rộng lớn về mặt mũi định nghĩa tuy nhiên nó hỗ trợ thật nhiều sức khỏe cho tới tất cả chúng ta. Khi technology PC canh ty những loài kiến trúc sư design những tòa mái ấm mới mẻ phát minh, hình dạng tam giác càng ngày càng trở thành thịnh hành như là 1 phần của những dự án công trình và là hình dạng chủ yếu cho tới một số trong những loại mái ấm cao tầng liền kề cũng như các vật tư xây đắp, vật dụng thiết kế bên trong. Năm 1989 bên trên Tokyo, Nhật Bản, những loài kiến trúc sư vẫn tự động chất vấn liệu rất có thể xây đắp một tòa tháp với trên 500 tầng nhằm hỗ trợ không khí văn chống ngân sách hợp lý và phải chăng cho tới TP.HCM sầm uất như vậy này hay là không. Nhưng sự nguy hại so với những tòa mái ấm kể từ trận động khu đất, những loài kiến trúc sư nhận định rằng hình dạng tam giác được xem là quan trọng, và vì vậy một tòa mái ấm hình tam giác đã và đang được xây đắp.

Tại TP.HCM Thành Phố New York, Lúc trải qua những quốc lộ rộng lớn, tao rất có thể bắt gặp nhiều những dự án công trình rộng lớn xây đắp theo như hình lăng trụ đứng đem lòng là tam giác. Ví dụ nổi bật vì vậy là Tòa mái ấm Flatiron hình tam giác nhưng mà quý khách quá nhận mang 1 không gian lận thiệt rất khó để đựng đồ vật thiết kế bên trong văn chống hiện tại đại tuy nhiên vấn đề này ko ngăn ngừa dự án công trình phát triển thành một hình tượng mang ý nghĩa sự thay đổi. Các mái ấm design đã trải nhà tại Na Uy bằng phương pháp dùng những chủ thể hình tam giác. Hình dạng tam giác đã và đang xuất hiện tại vô thánh địa cũng như các tòa mái ấm công nằm trong bao hàm những ngôi trường ĐH na ná tương hỗ cho những kiểu design mái ấm phát minh không chỉ có thế.

Cấu trúc của một hình tam giác vô cùng kiên cố chắn^[2], trong những khi cơ cấu hình của những nhiều giác không giống rất có thể bị thực hiện chênh chếch lên đường (ví dụ một hình chữ nhật rất có thể bị bẻ chênh chếch trở nên hình bình hành) kể từ áp suất cho tới những điểm vô nó, hình tam giác đem sức khỏe bất ngờ tương hỗ những cấu hình ngăn chặn những áp lực đè nén mặt mũi. Một hình tam giác sẽ không còn khi nào thay cho thay đổi hình dạng trừ Lúc những cạnh của chính nó bị uốn nắn cong, không ngừng mở rộng hoặc gãy hoặc nếu như những khớp của chính nó bị gãy. Về thực chất, từng một cạnh vô tam giác đều tương hỗ cho tới nhị cạnh sót lại. Một hình chữ nhật, ngược lại, dựa vào nhiều hơn thế nữa vô sức khỏe của những khớp theo gót nghĩa cấu hình. Một số mái ấm design phát minh vẫn lời khuyên thực hiện cho tới gạch men không chỉ có đem hình dạng văn bản nhật, và với hình dạng tam giác rất có thể được phối hợp theo gót phụ vương chiều. Rất đem kĩ năng những hình tam giác sẽ tiến hành dùng ngày rộng rãi theo gót những cơ hội mới mẻ Lúc loài kiến trúc tăng mức độ phức tạp. Điều cần thiết nên nhớ là hình tam giác cực mạnh về phỏng cứng, tuy nhiên trong những khi được bố trí theo như hình tam giác bố trí ko mạnh như hình lục giác Lúc bị (do cơ sự thịnh hành của những hình lục giác vô tự động nhiên).